This package is a polyhedra database based on the poly package found on https://netlib.org/polyhedra/ (Original Help message), and the polyhedra definitions found on http://dmccooey.com/polyhedra/. As such, Rpolyhedra provides with the following:
| Release | Usage | Development |
|---|---|---|
 |
||
Through Rpolyhedraexplorer you can navigate the polyhedra database without actually installing R environment.
install.packages("Rpolyhedra")Install the R package using the following commands on the R console:
devtools::install_github("ropensci/Rpolyhedra", build_opts = NULL)library(Rpolyhedra)# if want to switch to fullDB in user filespace, it will ask you for downloading the full database to your home directory
switchToFullDatabase()To get started execute the following commands:
# 0. Load libraries
library(knitr)
library(rgl)
# For foarding webgl output to knitr
knit_hooks$set(webgl = hook_webgl)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
# 1. Obtain 5 regular solids
polyhedra.2.draw <- getAvailablePolyhedra(source = "netlib")
polyhedra.2.draw <- polyhedra.2.draw %>%
filter(scraped.name %in%
c("tetrahedron", "octahedron", "cube",
"icosahedron", "dodecahedron"))
# 2. Setup colors and scales
n <- nrow(polyhedra.2.draw)
polyhedron.colors <- rainbow(n)
polyhedron.scale <- 5# For interactive RGL window
#```{r, render, webgl=TRUE}
# 3. open and setup RGL window
open3d()
#> glX
#> 1
par3d(FOV = 1)
rgl.bg( sphere =FALSE, fogtype = "none", color=c("black"))
rgl.viewpoint(theta = 0, phi=0, zoom=0.8, fov=1)
# 4. for each polyhedron, setup rotation, position and render
for (i in seq_len(n)) {
# Obtain polyhedron
polyhedron.row <- polyhedra.2.draw[i,]
polyhedron.name <- polyhedron.row$scraped.name
polyhedron <- getPolyhedron(source = polyhedron.row$source, polyhedron.name)
# Setup angles, position into transformationMatrix
current.angle <- i/n * 2 * pi
tm <- rotationMatrix(current.angle, 1, 0, 0)
x.pos <- round(polyhedron.scale * sin(current.angle), 2)
y.pos <- round(polyhedron.scale * cos(current.angle), 2)
tm <- tm %*% translationMatrix(x.pos, y.pos, 0)
# Render
print(paste("Drawing ", polyhedron.name, " rotated ", round(current.angle, 2),
" in (1,0,0) axis. Translated to (", x.pos, ",", y.pos, ",0)",
" with color ", polyhedron.colors[i], sep = ""))
shape.rgl <- polyhedron$getRGLModel(transformation.matrix = tm)
shade3d(shape.rgl, color = polyhedron.colors[i])
}
#> [1] "Drawing tetrahedron rotated 1.26 in (1,0,0) axis. Translated to (4.76,1.55,0) with color #FF0000"
#> [1] "Drawing octahedron rotated 2.51 in (1,0,0) axis. Translated to (2.94,-4.05,0) with color #CCFF00"
#> [1] "Drawing cube rotated 3.77 in (1,0,0) axis. Translated to (-2.94,-4.05,0) with color #00FF66"
#> [1] "Drawing icosahedron rotated 5.03 in (1,0,0) axis. Translated to (-4.76,1.55,0) with color #0066FF"
#> [1] "Drawing dodecahedron rotated 6.28 in (1,0,0) axis. Translated to (0,5,0) with color #CC00FF"
#rgl::rglwidget()
#rgl::rgl.snapshot("man/figures/README-5-polyhedra.png")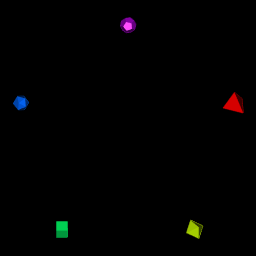
Includes 142 polyhedra definitions. The PHD format was created to describe the geometric polyhedron definitions derived mathematically by Andrew Hume and by the Kaleido program of Zvi Har’El.
PHD files were generated using poly2 library (no longer maintained). Although the code is available, specific programming skills are required to run it.
PHD files can be found in
extdata/netlib.org/polyhedra/index.html
Includes 767 polyhedra definitions. The polyhedra database built by David Mccooey has an open format which has been scraped to feed Rpolyhedra database
dmccooey files can be found in
extdata/dmccooey.com/polyhedra/
apt-get install libcurl4-openssl-devrun end user CRAN version
brew install opensslAfter, in R:
install.packages("devtools")sudo apt-get install r-cran-rglPlease note that the ‘Rpolyhedra’ project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.