



The oppr R package is decision support tool for prioritizing conservation projects. Prioritizations can be developed by maximizing expected feature richness, expected phylogenetic diversity, the number of features that meet persistence targets, or identifying a set of projects that meet persistence targets for minimal cost. Constraints (e.g. lock in specific actions) and feature weights can also be specified to further customize prioritizations. After defining a project prioritization problem, solutions can be obtained using exact algorithms, heuristic algorithms, or random processes. In particular, it is recommended to install the ‘Gurobi’ optimizer because it can identify optimal solutions very quickly. Finally, methods are provided for comparing different prioritizations and evaluating their benefits.
The latest official version of the oppr R package can be installed from the Comprehensive R Archive Network (CRAN) using the following R code.
install.packages("oppr", repos = "https://cran.rstudio.com/")Alternatively, the latest development version can be installed from GitHub using the following code. Please note that while developmental versions may contain additional features not present in the official version, they may also contain coding errors.
if (!require(remotes)) install.packages("remotes")
remotes::install_github("prioritizr/oppr")To cite the oppr R package in publications, please use:
Hanson JO, Schuster R, Strimas-Mackey M & Bennett JR (2019) Optimality in prioritizing conservation projects. Methods in Ecology & Evolution, 10: 1655–1663.
You can also use the following R code to determine which
version you have installed: packageVersion("oppr")
Here we will provide a short example showing how the oppr R package can be used to prioritize funding for conservation projects. To start off, we will set the seed for the random number generator to ensure you get the same results as shown here, and load the oppr R package.
set.seed(500)
library(oppr)Now we will load some data sets that are distributed with the
package. First, we will load the sim_features object. This
table contains information on the conservation features (e.g. species).
Specifically, each row corresponds to a different feature, and each
column contains information associated with the features. In this table,
the "name" column contains the name of each feature, and
the "weight" column denotes the relative importance for
each feature.
# load data
data(sim_features)
# print table
print(sim_features)## # A tibble: 5 × 2
## name weight
## <chr> <dbl>
## 1 F1 0.211
## 2 F2 0.211
## 3 F3 0.221
## 4 F4 0.630
## 5 F5 1.59Next, we will load the sim_actions object. This table
stores information about the various management actions
(i.e. tibble). Each row corresponds to a different action,
and each column describes different properties associated with the
actions. These actions correspond to specific management actions that
have known costs. For example, they may relate to pest eradication
activities (e.g. trapping) in sites of conservation importance. In this
table, the "name" column contains the name of each action,
and the "cost" column denotes the cost of each action. It
also contains additional columns for customizing the solutions, but we
will ignore them for now. Note that the last action—the
"baseline_action"—has a zero cost and is used with the a
baseline project (see below).
# load data
data(sim_actions)
# print table
print(sim_actions)## # A tibble: 6 × 4
## name cost locked_in locked_out
## <chr> <dbl> <lgl> <lgl>
## 1 F1_action 94.4 FALSE FALSE
## 2 F2_action 101. FALSE FALSE
## 3 F3_action 103. TRUE FALSE
## 4 F4_action 99.2 FALSE FALSE
## 5 F5_action 99.9 FALSE TRUE
## 6 baseline_action 0 FALSE FALSEAdditionally, we will load the sim_projects object. This
table stores information about various conservation projects. Each row
corresponds to a different project, and each column describes various
properties associated with the projects. These projects correspond to
groups of conservation actions. For example, a conservation project may
pertain to a set of conservation actions that relate to a single feature
or single geographic locality. In this table, the "name"
column contains the name of each project, the "success"
column denotes the probability of each project succeeding if it is
funded, the "F1"–"F5" columns show the
probability of each feature is expected to persist if each project is
funded (NA values mean that a feature does not benefit from
a project), and the "F1_action"–"F5_action"
columns indicate which actions are associated with which projects. Note
that the last project—the "baseline_project"—is associated
with the "baseline_action" action. This project has a zero
cost and represents the baseline probability of each feature persisting
if no other project is funded. This is important because we can’t find a
cost-effective solution if we don’t know how much better each project
improves a species’ chance at persistence. Finally, although most
projects in this example directly relate to a single feature, you can
input projects that directly affect the persistence of multiple
features.
# load data
data(sim_projects)
# print table
print(sim_projects, width = Inf)## # A tibble: 6 × 13
## name success F1 F2 F3 F4 F5 F1_action
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <lgl>
## 1 F1_project 0.919 0.791 NA NA NA NA TRUE
## 2 F2_project 0.923 NA 0.888 NA NA NA FALSE
## 3 F3_project 0.829 NA NA 0.502 NA NA FALSE
## 4 F4_project 0.848 NA NA NA 0.690 NA FALSE
## 5 F5_project 0.814 NA NA NA NA 0.617 FALSE
## 6 baseline_project 1 0.298 0.250 0.0865 0.249 0.182 FALSE
## F2_action F3_action F4_action F5_action baseline_action
## <lgl> <lgl> <lgl> <lgl> <lgl>
## 1 FALSE FALSE FALSE FALSE FALSE
## 2 TRUE FALSE FALSE FALSE FALSE
## 3 FALSE TRUE FALSE FALSE FALSE
## 4 FALSE FALSE TRUE FALSE FALSE
## 5 FALSE FALSE FALSE TRUE FALSE
## 6 FALSE FALSE FALSE FALSE TRUEAfter loading the data, we can begin formulating the project prioritization problem. Here our goal is to maximize the overall probability that each feature is expected to persist into the future (i.e. the feature richness), whilst also accounting for the relative importance of each feature and the fact that our resources are limited such that we can only spend at most $400 on funding management actions. Now, let’s build a project prioritization problem object that represents our goal.
# build problem
p <- problem(projects = sim_projects, actions = sim_actions,
features = sim_features, project_name_column = "name",
project_success_column = "success", action_name_column = "name",
action_cost_column = "cost", feature_name_column = "name") %>%
add_max_richness_objective(budget = 400) %>%
add_feature_weights(weight = "weight") %>%
add_binary_decisions() %>%
add_default_solver(verbose = FALSE)
# print problem
print(p)## Project Prioritization Problem
## actions F1_action, F2_action, F3_action, ... (6 actions)
## projects F1_project, F2_project, F3_project, ... (6 projects)
## features F1, F2, F3, ... (5 features)
## action costs: min: 0, max: 103.22583
## project success: min: 0.81379, max: 1
## objective: Maximum richness objective [budget (400)]
## targets: none
## weights: min: 0.21136, max: 1.59167
## decisions Binary decision
## constraints: <none>
## solver: Gurobi [first_feasible (0), gap (0), number_solutions (1), presolve (2), solution_pool_method (2), threads (1), time_limit (2147483647), time_limit (2147483647), verbose (0)]Next, we can solve this problem to obtain a solution. By default, we will obtain the optimal solution to our problem using an exact algorithm solver (e.g. using Gurobi or lpSolveAPI).
# solve problem
s <- solve(p)# print solution
print(s, width = Inf)## # A tibble: 1 × 21
## solution status obj cost F1_action F2_action F3_action F4_action F5_action
## <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 OPTIMAL 1.75 395. 1 1 0 1 1
## baseline_action F1_project F2_project F3_project F4_project F5_project
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 1 1 0 1 1
## baseline_project F1 F2 F3 F4 F5
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 0.808 0.865 0.0865 0.688 0.592The s table contains the solution and also various
statistics associated with the solution. Here, each row corresponds to a
different solution. Specifically, the "solution" column
contains an identifier for the solution (which may be useful for methods
that output multiple solutions), the "obj" column contains
the objective value (i.e. the expected feature richness for this
problem), the "cost" column stores the cost of the
solution, and the "status" column contains information from
the solver about the solution. Additionally, it contains columns for
each action ("F1_action", "F2_actions",
"F3_actions", …, "baseline_action") which
indicate if each action was prioritized for funding in the solution.
Additionally, it contains columns for each project
("F1_project", "F2_project",
"F3_project", …, "baseline_project") that
indicate if the project was completely funded or not. Finally, it
contains column for each feature ("F1, "F2",
"F3, …) which indicate the probability that each feature is
expected to persist into the future under each solution (for information
on how this is calculated see ?add_max_richness_objective).
Since tabular data can be difficult to understand, let’s visualize how
well this solution would conserve the features. Note that features which
benefit from fully funded projects, excepting the baseline project, are
denoted with an asterisk.
# visualize solution
plot(p, s)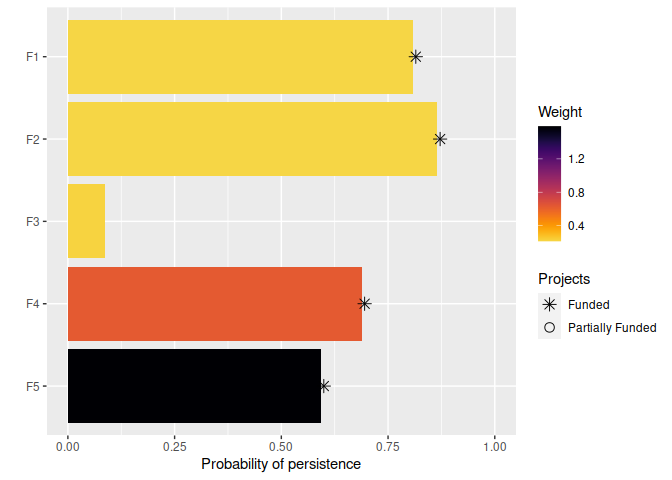
This has just been a taster of the oppr R package. For more information, see the package vignette.
If you have any questions about using the oppr R package or suggestions for improving it, please file an issue at the package’s online code repository.